
Ucz się
matematyki w
szkole matemagii
Wciąż zostajesz w tyle?

Magia zrozumienia

Magia zrozumienia

Online, który wciąga
Uczymy tak, żeby dziecko rozumiało
Żywe wyjaśnienie 1:1
Nauczyciel nie czyta materiału — prowadzi dialog. Wyjaśnia przez przykłady, zadaje pytania, rysuje schematy, dostosowuje się do tempa dziecka.
Bez presji

Uczniom podoba się format
Interaktywne zajęcia — w rytmie współczesnego dziecka
Lekcje są zaprojektowane tak, żeby utrzymać zainteresowanie. Dzieci czują postęp już po pierwszych zajęciach — i chcą kontynuować.
Wideorozmowa + interaktywność

Wsparcie między lekcjami
Dziecko nie zostaje samo z trudnym tematem. Asystent AI pomaga zrozumieć krok po kroku, a nauczyciel — wspiera i podpowiada właściwy kierunek.
Online, który wciąga
Uczymy tak, żeby dziecko rozumiało
Żywe wyjaśnienie 1:1
Nauczyciel nie czyta materiału — prowadzi dialog. Wyjaśnia przez przykłady, zadaje pytania, rysuje schematy, dostosowuje się do tempa dziecka.
Bez presji

Uczniom podoba się format
Interaktywne zajęcia — w rytmie współczesnego dziecka
Lekcje są zaprojektowane tak, żeby utrzymać zainteresowanie. Dzieci czują postęp już po pierwszych zajęciach — i chcą kontynuować.
Wideorozmowa + interaktywność

Wsparcie między lekcjami
Dziecko nie zostaje samo z trudnym tematem. Asystent AI pomaga zrozumieć krok po kroku, a nauczyciel — wspiera i podpowiada właściwy kierunek.

Droga do wyniku — prostymi krokami
To nie abstrakcyjne "zajęcia co tydzień" — to osobista ścieżka, którą dziecko przechodzi razem z korepetytorem i asystentem AI

Lekcja zapoznawcza

Badamy logikę myślenia dziecka, luki i mocne strony. W lekkiej, inspirującej atmosferze — jak przyjacielska rozmowa, nie sprawdzian.
Zapisz sięOsobisty plan działania

Tworzymy konkretny plan: co uczyć, w jakiej kolejności, na co kłaść nacisk. Żadnego chaosu — tylko jasna logika i struktura, łatwa do przejścia.
Zapisz sięLekcje 1:1 + asystent AI + quizy

Dziecko uczy się w żywym dialogu z korepetytorem, a między lekcjami utrwala materiał w formie: krótkich quizów, wyjaśnień asystenta AI, mikro-zadań.
Zapisz sięWidoczny postęp
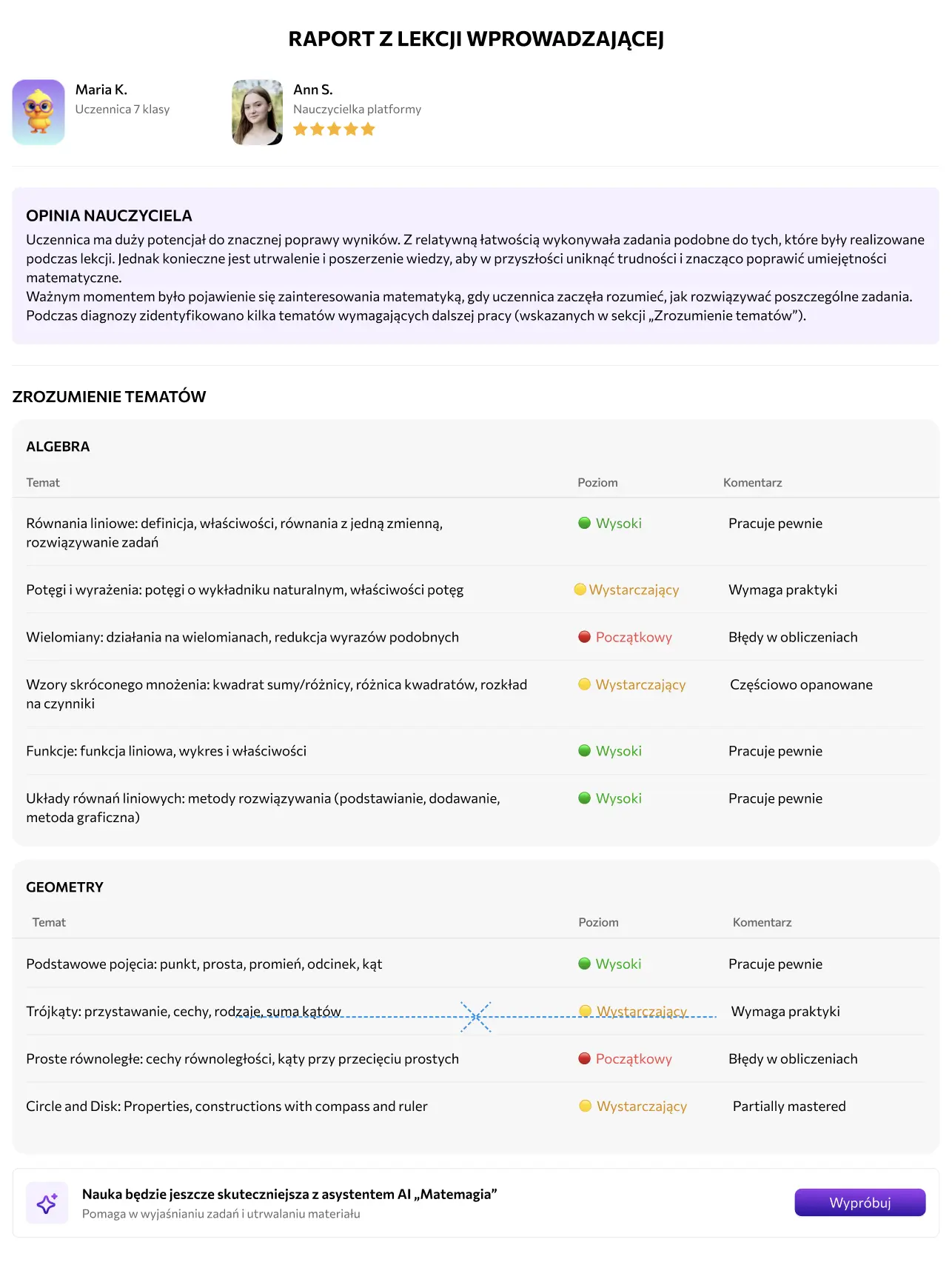

Rodzice otrzymują krótki raport: co zrobiono, jakie sukcesy, rekomendacje. A dziecko widzi, że może więcej, niż myślało.
Zapisz sięAsystent AI: wyjaśni, podpowie, wesprze
To jak mieć osobistego nauczyciela 24/7: pytasz i od razu dostajesz zrozumiałe wyjaśnienie. Bez stresu. Bez pośpiechu. W tempie dziecka
Asystent AI: wyjaśni, podpowie, wesprze
To jak mieć osobistego nauczyciela 24/7: pytasz i od razu dostajesz zrozumiałe wyjaśnienie. Bez stresu. Bez pośpiechu. W tempie dziecka
Quizy — łatwe utrwalanie wiedzy, które uczniowie uwielbiają



Krótkie, interaktywne, zaprojektowane tak, aby dziecko nie tylko przypominało sobie materiał, ale czuło małe zwycięstwo za każdym razem, gdy odpowie "dobrze"
✅ 3–5 minut — i temat utrwalony
Idealne, żeby szybko przypomnieć sobie temat lub sprawdzić się po pracach domowych
😎 Pomyliłeś się? Otrzymaj wyjaśnienie
Błędy tu nie są straszne — prowadzą do "aha, teraz rozumiem!"
🚀 Codzienny nawyk, który przynosi tak wiele korzyści
Małe kroki, które budują pewność siebie.
Quizy — łatwe utrwalanie wiedzy, które uczniowie uwielbiają
Krótkie, interaktywne, zaprojektowane tak, aby dziecko nie tylko przypominało sobie materiał, ale czuło małe zwycięstwo za każdym razem, gdy odpowie "dobrze"
✅ 3–5 minut — i temat utrwalony
Idealne, żeby szybko przypomnieć sobie temat lub sprawdzić się po pracach domowych
😎 Pomyliłeś się? Otrzymaj wyjaśnienie
Błędy tu nie są straszne — prowadzą do "aha, teraz rozumiem!"
🚀 Codzienny nawyk, który przynosi tak wiele korzyści
Małe kroki, które budują pewność siebie.
Mathema kształtuje nawyk pewnego myślenia
Krótkie quizy, porady asystenta AI, regularne lekcje — to system, który kształtuje nie tylko oceny, ale matemagiczne myślenie.

Umiejętność logicznego myślenia — uniwersalna supermoc

Komfortowe tempo, spersonalizowane podejście

Uczucie zwycięstwa: każde "dobrze!" — jak mały sukces
Mathema kształtuje nawyk pewnego myślenia
Krótkie quizy, porady asystenta AI, regularne lekcje — to system, który kształtuje nie tylko oceny, ale matemagiczne myślenie.

Umiejętność logicznego myślenia — uniwersalna supermoc

Komfortowe tempo, spersonalizowane podejście

Uczucie zwycięstwa: każde "dobrze!" — jak mały sukces
Dobierzemy matemaga, który odkryje wewnętrzną matematyczną siłę
Dobierzemy matemaga, który odkryje wewnętrzną matematyczną siłę
Gdy matematyka staje się zrozumiała — zmiany widać od razu
Syn jest bardzo zadowolony z zajęć z panem Julianem. Uzupełnił luki w wiedzy i bez problemu opanowuje każdy temat. Polecamy w 100%
Polecam pełen profesjonalizm i indywidualne podejście
Nauczycielka godna polecenia potrafi stworzyć indywidualną relacje z uczniem motywującą go do nauki , uczeń czuje wsparcie w nauczycielce.
Dla mojego syna bardzo dobry nauczyciel bardzo dobrze i zrozumiałe tłumaczy zadania u mojego syna widać różnicę i poprawę ocen jestem zadowolona
Polecam!! Dziecko zadowolone, z chętnie odwiedza zajęcia!!
Pan Julian to wspaniały nauczyciel ma bardzo dobre podejście do nauki, jest humorystyczny, miły, Dobrze tłumaczy zadania i też daje ciekawostki związane z omawianym tematem, dobrze przygotowuję przed sprawdzianem, testem lub kartkówką, Polecam. Mateusz
Szczerze polecam Pana Konrada jako korepetytora matematyki. Przygotowuję się do matury i mam naprawdę ogromne braki wiedzy. Mimo że odbyliśmy dopiero około trzech lekcji, już w tak krótkim czasie udało mu się wyjaśnić mi wiele rzeczy, z którymi wcześniej zupełnie sobie nie dawałem rady i nie mogłem zrozumieć
Jesteśmy bardzo zadowoleni z tej formy nauki. Zajęcia są prowadzone w sposób jasny i zrozumiały, a materiał tłumaczony cierpliwie i dokładnie. Wysoki poziom, dostrzeganie i rozwijanie potencjału ucznia, umiejętność zaciekawienia. Pani Kasia jest świetnym nauczycielem!
Jest niesamowitą nauczycielką, która zawsze motywuje. Prowadzone zajęcia są ciekawe, urozmaicone i motywujące Kaśkę do aktywnego udziału. Dodatkowo, doceniam otwartość na współpracę, rzetelne informuje o postępach córki.
Mój syn od pewnego czasu uczestniczy w lekcjach matematyki w formie online. Jesteśmy bardzo zadowoleni z tej formy nauki. Zajęcia są prowadzone w sposób jasny i zrozumiały, a materiał tłumaczony cierpliwie i dokładnie. Dzięki regularnym spotkaniom syn lepiej rozumie bieżący materiał szkolny, jest pewniejszy siebie podczas sprawdzianów. Bardzo polecam lekcje z Panią Natalią!
Pan Julian, jest nauczycielem pełnym pozytywnej energii co pomaga mi polubić uczenie się matematyki. Potrafi z dużą cierpliwością wytłumaczyć materiał.Bardzo lubię z nim zajęcia. Uczennica- Julia.
Z pełnym przekonaniem polecam zajęcia z Panią Natalią. Dzięki jej pracy córka przeszła ogromną zmianę. Jeszcze niedawno na samo słowo „matematyka” reagowała łzami, dziś podchodzi do niej spokojniej i z większą wiarą w siebie. Pani Natalia pracuje indywidualnie, z wyczuciem i cierpliwością. Potrafi zainteresować tematem i zachęcić do nauki bez presji. Dziękujemy za przywrócenie wiary we własne możliwości.
Bardzo polecam panią Natalię, dzięki niej zrobiłam spory progres i poprawiłam oceny.Atmosfera na lekcjach super i bezstresowo☺️ serdecznie polecam!
Pełen profesjonalizm. Córka jest bardzo zadowolona z zajęć 🙂 Cyt. "Pani wszystko spokojnie tłumaczy".
Syn skończył lekcję z entuzjazmem , co nie często się zdarza . Nie tylko zrozumiał lekcję co nie było to dla niego nudne ani trudne
Moi synowi pracują z Panem Norbertem od ok. 6 miesięcy i wszyscy jesteśmy bardzo zadowoleni. Dzieciaki bardzo szybko usystematyzowały swoją matematyczną wiedzę i zrozumiały dotychczas niejasne, bądź bardziej skomplikowane tematy. Obaj chętnie uczestniczą w lekcjach, a po zakończonych zajęciach zawsze widać w nich satysfakcję. Z mojej strony jako rodzica bardzo dziękuję za doskonały kontakt i współpracę. Bardzo serdecznie polecam,
Bardzo dobry nauczyciel z pasją podchodzi do lekcji potrafi zachęcić ucznia do matematyki.
To była nasza pierwsza lekcja z Natalią i NA PEWNO nie ostatnia. Wspaniałe podejście do ucznia. Stosowanie wielu metod nauczania w zależności od potrzeb na daną chwilę. Podpowiadanie trików w razie potrzeby, które uczeń może zastosować w stresujących sytuacjach. Wspaniała osoba i wspaniały nauczyciel.
polecam bardzo pana krystiana, nie stresuje mnie jak jego poprzednicy i ma ogromna cierpliwość (;
Matematyka z tym nauczycielem to sama przyjemność. Jest super. Odkąd syn zaczął się z nim uczyć, to nie może się doczekać kolejnej lekcji.
Pan Adam wyróżnia się ogromną cierpliwością oraz zaangażowaniem. Skutecznie motywuje do pracy i rozwijania umiejętności. Lekcje odbywają się w spokojnej i przyjaznej atmosferze, co sprawia, że nie boje zadawać się pytań. Dzięki jego wsparciu matematyka staje się bardziej zrozumiała :).
Nauczycielka bardzo sympatyczna z świetnym podejściem do Córki. Oliwia bardzo zadowolona z lekcji diagnostycznej. Pierwszy raz od razu zrozumiała tłumaczenia p. Nauczycielki. Kontynuujemy dalszą naukę z panią Natalią.
Polecam lekcje z Panem Maciejem. Syn miał trudności w szkole, był bardzo zniechęcony co matematyki. Po kilku lekcjach nastąpiła ogromna zmiana w jego podejściu do zadań, chętnie pracował i ma poprawioną ocenę na semestr 🤩 wzrosła jego samoocena i wiara w siebie, chęć do matmy, co przy adhd nie jest tak łatwe do osiągnięcia. Także bardzo polecamy mathema.me z Panem Maciejem.
Syn jest po pierwszej lekcji i jest zadowolony bardzo miła i sympatyczna pani ma podejście do ucznia polecam
Syn bardzo zadowolony z korepetycji i zaproponował lekcje 2x w tygodniu.
Pan Jakub to znakomity nauczyciel matematyki, który wyróżnia się ogromnym zaangażowaniem i pasją do nauczania. Potrafi w przystępny sposób tłumaczyć nawet najtrudniejsze zagadnienia, dzięki czemu lekcje są zrozumiałe i ciekawe. Zawsze jest cierpliwy, pomocny i życzliwy wobec uczniów, motywując ich do pracy i wiary we własne możliwości. Dzięki niemu matematyka staje się logiczna, mniej stresująca i naprawdę interesująca.
Pan Prowadzący ma świetne podejście do dzieci - potrafi rewelacyjnie tłumaczyć w sposób prosty i rzeczowy, ma anielską cierpliwość. Synek zachwycony! Zdecydowanie baaardzo polecam!
lekcje nie wywołują stresu. zadania są dobrane w idealny sposób. W prosty sposób wytłumacza ciężkie rzeczy. W miłej atmosferze są prowadzone zajęcia
Syn jest bardzo zadowolony z zajęć z panem Julianem. Uzupełnił luki w wiedzy i bez problemu opanowuje każdy temat. Polecamy w 100%
Polecam pełen profesjonalizm i indywidualne podejście
Nauczycielka godna polecenia potrafi stworzyć indywidualną relacje z uczniem motywującą go do nauki , uczeń czuje wsparcie w nauczycielce.
Dla mojego syna bardzo dobry nauczyciel bardzo dobrze i zrozumiałe tłumaczy zadania u mojego syna widać różnicę i poprawę ocen jestem zadowolona
Polecam!! Dziecko zadowolone, z chętnie odwiedza zajęcia!!
Pan Julian to wspaniały nauczyciel ma bardzo dobre podejście do nauki, jest humorystyczny, miły, Dobrze tłumaczy zadania i też daje ciekawostki związane z omawianym tematem, dobrze przygotowuję przed sprawdzianem, testem lub kartkówką, Polecam. Mateusz
Szczerze polecam Pana Konrada jako korepetytora matematyki. Przygotowuję się do matury i mam naprawdę ogromne braki wiedzy. Mimo że odbyliśmy dopiero około trzech lekcji, już w tak krótkim czasie udało mu się wyjaśnić mi wiele rzeczy, z którymi wcześniej zupełnie sobie nie dawałem rady i nie mogłem zrozumieć
Jesteśmy bardzo zadowoleni z tej formy nauki. Zajęcia są prowadzone w sposób jasny i zrozumiały, a materiał tłumaczony cierpliwie i dokładnie. Wysoki poziom, dostrzeganie i rozwijanie potencjału ucznia, umiejętność zaciekawienia. Pani Kasia jest świetnym nauczycielem!
Jest niesamowitą nauczycielką, która zawsze motywuje. Prowadzone zajęcia są ciekawe, urozmaicone i motywujące Kaśkę do aktywnego udziału. Dodatkowo, doceniam otwartość na współpracę, rzetelne informuje o postępach córki.
Mój syn od pewnego czasu uczestniczy w lekcjach matematyki w formie online. Jesteśmy bardzo zadowoleni z tej formy nauki. Zajęcia są prowadzone w sposób jasny i zrozumiały, a materiał tłumaczony cierpliwie i dokładnie. Dzięki regularnym spotkaniom syn lepiej rozumie bieżący materiał szkolny, jest pewniejszy siebie podczas sprawdzianów. Bardzo polecam lekcje z Panią Natalią!
Pan Julian, jest nauczycielem pełnym pozytywnej energii co pomaga mi polubić uczenie się matematyki. Potrafi z dużą cierpliwością wytłumaczyć materiał.Bardzo lubię z nim zajęcia. Uczennica- Julia.
Z pełnym przekonaniem polecam zajęcia z Panią Natalią. Dzięki jej pracy córka przeszła ogromną zmianę. Jeszcze niedawno na samo słowo „matematyka” reagowała łzami, dziś podchodzi do niej spokojniej i z większą wiarą w siebie. Pani Natalia pracuje indywidualnie, z wyczuciem i cierpliwością. Potrafi zainteresować tematem i zachęcić do nauki bez presji. Dziękujemy za przywrócenie wiary we własne możliwości.
Bardzo polecam panią Natalię, dzięki niej zrobiłam spory progres i poprawiłam oceny.Atmosfera na lekcjach super i bezstresowo☺️ serdecznie polecam!
Pełen profesjonalizm. Córka jest bardzo zadowolona z zajęć 🙂 Cyt. "Pani wszystko spokojnie tłumaczy".
Syn skończył lekcję z entuzjazmem , co nie często się zdarza . Nie tylko zrozumiał lekcję co nie było to dla niego nudne ani trudne
Moi synowi pracują z Panem Norbertem od ok. 6 miesięcy i wszyscy jesteśmy bardzo zadowoleni. Dzieciaki bardzo szybko usystematyzowały swoją matematyczną wiedzę i zrozumiały dotychczas niejasne, bądź bardziej skomplikowane tematy. Obaj chętnie uczestniczą w lekcjach, a po zakończonych zajęciach zawsze widać w nich satysfakcję. Z mojej strony jako rodzica bardzo dziękuję za doskonały kontakt i współpracę. Bardzo serdecznie polecam,
Bardzo dobry nauczyciel z pasją podchodzi do lekcji potrafi zachęcić ucznia do matematyki.
To była nasza pierwsza lekcja z Natalią i NA PEWNO nie ostatnia. Wspaniałe podejście do ucznia. Stosowanie wielu metod nauczania w zależności od potrzeb na daną chwilę. Podpowiadanie trików w razie potrzeby, które uczeń może zastosować w stresujących sytuacjach. Wspaniała osoba i wspaniały nauczyciel.
polecam bardzo pana krystiana, nie stresuje mnie jak jego poprzednicy i ma ogromna cierpliwość (;
Matematyka z tym nauczycielem to sama przyjemność. Jest super. Odkąd syn zaczął się z nim uczyć, to nie może się doczekać kolejnej lekcji.
Pan Adam wyróżnia się ogromną cierpliwością oraz zaangażowaniem. Skutecznie motywuje do pracy i rozwijania umiejętności. Lekcje odbywają się w spokojnej i przyjaznej atmosferze, co sprawia, że nie boje zadawać się pytań. Dzięki jego wsparciu matematyka staje się bardziej zrozumiała :).
Nauczycielka bardzo sympatyczna z świetnym podejściem do Córki. Oliwia bardzo zadowolona z lekcji diagnostycznej. Pierwszy raz od razu zrozumiała tłumaczenia p. Nauczycielki. Kontynuujemy dalszą naukę z panią Natalią.
Polecam lekcje z Panem Maciejem. Syn miał trudności w szkole, był bardzo zniechęcony co matematyki. Po kilku lekcjach nastąpiła ogromna zmiana w jego podejściu do zadań, chętnie pracował i ma poprawioną ocenę na semestr 🤩 wzrosła jego samoocena i wiara w siebie, chęć do matmy, co przy adhd nie jest tak łatwe do osiągnięcia. Także bardzo polecamy mathema.me z Panem Maciejem.
Syn jest po pierwszej lekcji i jest zadowolony bardzo miła i sympatyczna pani ma podejście do ucznia polecam
Syn bardzo zadowolony z korepetycji i zaproponował lekcje 2x w tygodniu.
Pan Jakub to znakomity nauczyciel matematyki, który wyróżnia się ogromnym zaangażowaniem i pasją do nauczania. Potrafi w przystępny sposób tłumaczyć nawet najtrudniejsze zagadnienia, dzięki czemu lekcje są zrozumiałe i ciekawe. Zawsze jest cierpliwy, pomocny i życzliwy wobec uczniów, motywując ich do pracy i wiary we własne możliwości. Dzięki niemu matematyka staje się logiczna, mniej stresująca i naprawdę interesująca.
Pan Prowadzący ma świetne podejście do dzieci - potrafi rewelacyjnie tłumaczyć w sposób prosty i rzeczowy, ma anielską cierpliwość. Synek zachwycony! Zdecydowanie baaardzo polecam!
lekcje nie wywołują stresu. zadania są dobrane w idealny sposób. W prosty sposób wytłumacza ciężkie rzeczy. W miłej atmosferze są prowadzone zajęcia
Pani Marta Tobolik tworzy pozytywną atmosferę podczas lekcji. Potrafi dostrzec braki i z dużą cierpliwością dąży do ich uzupełnienia. Mój syn chętnie bierze udział w lekcjach i mówi, że Pani Marta dobrze tłumaczy. Polecam Panią Martę Tobolik jako nauczyciela matematyki.
Polecam.
Z całego serca polecam tego nauczyciela. Zajęcia są prowadzone w przyjaznej i bezstresowej atmosferze, a materiał tłumaczony jasno, cierpliwie i w sposób dopasowany do ucznia. Dzięki korepetycjom zauważyłam realne postępy. Nauczyciel jest zaangażowany, punktualny i zawsze dobrze przygotowany. Zdecydowanie warto!
Bardzo dobry korepetytor z matematyki — tłumaczy jasno, cierpliwie i krok po kroku. Potrafi w prosty sposób wyjaśnić nawet trudne zagadnienia i zawsze upewnia się, że materiał jest zrozumiały.
Bardzo polecam ! Świetne podejście do ucznia, wszystko tłumaczone jasno i cierpliwie. Zajęcia są dobrze zorganizowane i naprawdę pomagają zrozumieć materiał.
Lekcja przebiegła w spokojnej i miłej atmosferze. Pani Natali zachęciła do pytań i otwartości. Emilka była bardzo zadowolona 🙂
Krystian korepetytor od matematyki jasno tłumaczy materiał i zawsze cierpliwie odpowiada na pytania. Na lekcjach panuje dobra i luzna atmosfera, dzięki łatwo się skupić i zrozumieć nowe zagadnienia.
Korepetytor tłumaczy w prosty i zrozumiały sposób, jasno, cierpliwie i z zaangażowaniem.
Pan Sebastian wyróżnia się ogromną cierpliwością i umiejętnością tłumaczenia trudnych zagadnień w prosty, zrozumiały sposób. Zajęcia zawsze są dobrze zorganizowane i prowadzone w przyjaznej atmosferze, dzięki czemu nauka staje się dużo łatwiejsza i bardziej motywująca. Polecam!
Pan Sebastian to bardzo dobry nauczyciel. Dzieki jego pracy, moj syn niw boi sie lekcji matematyki no i oceny znacznie ulwgly poprawie. Bardzo polecam, bardzo kompetentny nauczyciel. Cala wiedza przekazana podczas lekcji zostaje w glowie ucznia😊
Cierpliwy, potrafi jasno i prosto wytłumaczyć materiał, oraz posiada bardzo przyjazne i bezstresowe podejście do ucznia
Ten czlowiek mnie ratuje z matematyki i ogolnie mega dobrze sie z nim pracuje bo jest cierpilwy oraz ma duza wiedze z tego przedmiotu
Szczerze polecam w szczególności Pana Kamila. Dokonał cudu 😀😃🙂, rozkochał w matematyce, wytlumaczył, nauczył i dodał pewności siebie wyjątkowemu "antymatematykowi", jeszcze raz szczerze polecam:)
Jestem bardzo zadowolona z zajęć w Mathema , a zwłaszcza za umiejętność przekazania wiedzy i zrozumiałe wytłumaczenie przez Pan Marcina Przegalińskiego. Dla syna to najlepszy nauczyciel matematyki jakiego do tej pory spotkał Lekcje przez Pana Marcina są prowadzone w bardzo przejrzysty sposób i na bardzo fajnych przykładach tłumaczy zadania. Polecamy naukę u Pana Marcina Przegalińskiego.
Bardzo fajnie przeprowadzona lekcja. Dziękuję w imieniu syna.
Uczeń zadowolony z lekcji, rozumie zagadnienia, jednak nie moze tego przełożyć na warunki szkolne.
Brak umiejętności jasnego tłumaczenia zadań. Brak przygotowania metodycznego. Prowadząca nie jest nauczycielem matematyki. Nie ma wykształcenie w tym kierunku.
Pani jest bardzo wspaniałą osobą, ma świetne podejście do mojego dziecka. Uczy na wysokim poziomie. Jest wymagająca, ale w dobrym znaczeniu tego słowa - potrafi wytłumaczyć w spokoju, tak by dziecko potrafiło wykonać zadanie samo z zaangażowaniem swojego myślenia. Jestem zadowolona jako matka, a Olga czeka z zaciekawieniem na każdą kolejną lekcje, a to jest najważniejsze !
Jasno i wyraźnie Pan Pawel przekazywał wiedzę, nawet jak potrzeba było kilka razy powtórzyć to bez nerwów powtarzał i wyjaśniał..
Dziękujemy Panu Adrianowi Kaczyńskiemu za profesjonalną lekcję. Córka jest bardzo zadowolona i zdecydowała się na współpracę z Panem Adrianem w uczeniu się matematyki. Magda
Relacja z uczniem i jakość prowadzenia zajęć.
Bardzo dobrze podejscie do dziecka. Dziękujemy bardzo.
Wspaniala oraz ciepła nauczycielka. Nauka z Panią Klaudia to sama przyjemność 🤩
Córce lekcja się podobała, z chęcią zobaczy się na kolejnych lekcjach z Panem Adrianem Dziękujemy :)
Polecam. Syn jest zadowolony, zajęcia są bezstresowe.
Pani Klaudia ma super podejście do młodzieży, swoim indywidualnym podejściem potrafi zainteresować każdego
Lekcja córce się bardzi podobała. Bardzo polecam.
Bardzo fajne pan cypian prowadzi zajęcia
Pani Marta Tobolik tworzy pozytywną atmosferę podczas lekcji. Potrafi dostrzec braki i z dużą cierpliwością dąży do ich uzupełnienia. Mój syn chętnie bierze udział w lekcjach i mówi, że Pani Marta dobrze tłumaczy. Polecam Panią Martę Tobolik jako nauczyciela matematyki.
Polecam.
Z całego serca polecam tego nauczyciela. Zajęcia są prowadzone w przyjaznej i bezstresowej atmosferze, a materiał tłumaczony jasno, cierpliwie i w sposób dopasowany do ucznia. Dzięki korepetycjom zauważyłam realne postępy. Nauczyciel jest zaangażowany, punktualny i zawsze dobrze przygotowany. Zdecydowanie warto!
Bardzo dobry korepetytor z matematyki — tłumaczy jasno, cierpliwie i krok po kroku. Potrafi w prosty sposób wyjaśnić nawet trudne zagadnienia i zawsze upewnia się, że materiał jest zrozumiały.
Bardzo polecam ! Świetne podejście do ucznia, wszystko tłumaczone jasno i cierpliwie. Zajęcia są dobrze zorganizowane i naprawdę pomagają zrozumieć materiał.
Lekcja przebiegła w spokojnej i miłej atmosferze. Pani Natali zachęciła do pytań i otwartości. Emilka była bardzo zadowolona 🙂
Krystian korepetytor od matematyki jasno tłumaczy materiał i zawsze cierpliwie odpowiada na pytania. Na lekcjach panuje dobra i luzna atmosfera, dzięki łatwo się skupić i zrozumieć nowe zagadnienia.
Korepetytor tłumaczy w prosty i zrozumiały sposób, jasno, cierpliwie i z zaangażowaniem.
Pan Sebastian wyróżnia się ogromną cierpliwością i umiejętnością tłumaczenia trudnych zagadnień w prosty, zrozumiały sposób. Zajęcia zawsze są dobrze zorganizowane i prowadzone w przyjaznej atmosferze, dzięki czemu nauka staje się dużo łatwiejsza i bardziej motywująca. Polecam!
Pan Sebastian to bardzo dobry nauczyciel. Dzieki jego pracy, moj syn niw boi sie lekcji matematyki no i oceny znacznie ulwgly poprawie. Bardzo polecam, bardzo kompetentny nauczyciel. Cala wiedza przekazana podczas lekcji zostaje w glowie ucznia😊
Cierpliwy, potrafi jasno i prosto wytłumaczyć materiał, oraz posiada bardzo przyjazne i bezstresowe podejście do ucznia
Ten czlowiek mnie ratuje z matematyki i ogolnie mega dobrze sie z nim pracuje bo jest cierpilwy oraz ma duza wiedze z tego przedmiotu
Szczerze polecam w szczególności Pana Kamila. Dokonał cudu 😀😃🙂, rozkochał w matematyce, wytlumaczył, nauczył i dodał pewności siebie wyjątkowemu "antymatematykowi", jeszcze raz szczerze polecam:)
Jestem bardzo zadowolona z zajęć w Mathema , a zwłaszcza za umiejętność przekazania wiedzy i zrozumiałe wytłumaczenie przez Pan Marcina Przegalińskiego. Dla syna to najlepszy nauczyciel matematyki jakiego do tej pory spotkał Lekcje przez Pana Marcina są prowadzone w bardzo przejrzysty sposób i na bardzo fajnych przykładach tłumaczy zadania. Polecamy naukę u Pana Marcina Przegalińskiego.
Bardzo fajnie przeprowadzona lekcja. Dziękuję w imieniu syna.
Uczeń zadowolony z lekcji, rozumie zagadnienia, jednak nie moze tego przełożyć na warunki szkolne.
Brak umiejętności jasnego tłumaczenia zadań. Brak przygotowania metodycznego. Prowadząca nie jest nauczycielem matematyki. Nie ma wykształcenie w tym kierunku.
Pani jest bardzo wspaniałą osobą, ma świetne podejście do mojego dziecka. Uczy na wysokim poziomie. Jest wymagająca, ale w dobrym znaczeniu tego słowa - potrafi wytłumaczyć w spokoju, tak by dziecko potrafiło wykonać zadanie samo z zaangażowaniem swojego myślenia. Jestem zadowolona jako matka, a Olga czeka z zaciekawieniem na każdą kolejną lekcje, a to jest najważniejsze !
Jasno i wyraźnie Pan Pawel przekazywał wiedzę, nawet jak potrzeba było kilka razy powtórzyć to bez nerwów powtarzał i wyjaśniał..
Dziękujemy Panu Adrianowi Kaczyńskiemu za profesjonalną lekcję. Córka jest bardzo zadowolona i zdecydowała się na współpracę z Panem Adrianem w uczeniu się matematyki. Magda
Relacja z uczniem i jakość prowadzenia zajęć.
Bardzo dobrze podejscie do dziecka. Dziękujemy bardzo.
Wspaniala oraz ciepła nauczycielka. Nauka z Panią Klaudia to sama przyjemność 🤩
Córce lekcja się podobała, z chęcią zobaczy się na kolejnych lekcjach z Panem Adrianem Dziękujemy :)
Polecam. Syn jest zadowolony, zajęcia są bezstresowe.
Pani Klaudia ma super podejście do młodzieży, swoim indywidualnym podejściem potrafi zainteresować każdego
Lekcja córce się bardzi podobała. Bardzo polecam.
Bardzo fajne pan cypian prowadzi zajęcia
Syn jest bardzo zadowolony z zajęć z panem Julianem. Uzupełnił luki w wiedzy i bez problemu opanowuje każdy temat. Polecamy w 100%
Polecam pełen profesjonalizm i indywidualne podejście
Nauczycielka godna polecenia potrafi stworzyć indywidualną relacje z uczniem motywującą go do nauki , uczeń czuje wsparcie w nauczycielce.
Dla mojego syna bardzo dobry nauczyciel bardzo dobrze i zrozumiałe tłumaczy zadania u mojego syna widać różnicę i poprawę ocen jestem zadowolona
Polecam!! Dziecko zadowolone, z chętnie odwiedza zajęcia!!
Pan Julian to wspaniały nauczyciel ma bardzo dobre podejście do nauki, jest humorystyczny, miły, Dobrze tłumaczy zadania i też daje ciekawostki związane z omawianym tematem, dobrze przygotowuję przed sprawdzianem, testem lub kartkówką, Polecam. Mateusz
Szczerze polecam Pana Konrada jako korepetytora matematyki. Przygotowuję się do matury i mam naprawdę ogromne braki wiedzy. Mimo że odbyliśmy dopiero około trzech lekcji, już w tak krótkim czasie udało mu się wyjaśnić mi wiele rzeczy, z którymi wcześniej zupełnie sobie nie dawałem rady i nie mogłem zrozumieć
Jesteśmy bardzo zadowoleni z tej formy nauki. Zajęcia są prowadzone w sposób jasny i zrozumiały, a materiał tłumaczony cierpliwie i dokładnie. Wysoki poziom, dostrzeganie i rozwijanie potencjału ucznia, umiejętność zaciekawienia. Pani Kasia jest świetnym nauczycielem!
Jest niesamowitą nauczycielką, która zawsze motywuje. Prowadzone zajęcia są ciekawe, urozmaicone i motywujące Kaśkę do aktywnego udziału. Dodatkowo, doceniam otwartość na współpracę, rzetelne informuje o postępach córki.
Mój syn od pewnego czasu uczestniczy w lekcjach matematyki w formie online. Jesteśmy bardzo zadowoleni z tej formy nauki. Zajęcia są prowadzone w sposób jasny i zrozumiały, a materiał tłumaczony cierpliwie i dokładnie. Dzięki regularnym spotkaniom syn lepiej rozumie bieżący materiał szkolny, jest pewniejszy siebie podczas sprawdzianów. Bardzo polecam lekcje z Panią Natalią!
Pan Julian, jest nauczycielem pełnym pozytywnej energii co pomaga mi polubić uczenie się matematyki. Potrafi z dużą cierpliwością wytłumaczyć materiał.Bardzo lubię z nim zajęcia. Uczennica- Julia.
Z pełnym przekonaniem polecam zajęcia z Panią Natalią. Dzięki jej pracy córka przeszła ogromną zmianę. Jeszcze niedawno na samo słowo „matematyka” reagowała łzami, dziś podchodzi do niej spokojniej i z większą wiarą w siebie. Pani Natalia pracuje indywidualnie, z wyczuciem i cierpliwością. Potrafi zainteresować tematem i zachęcić do nauki bez presji. Dziękujemy za przywrócenie wiary we własne możliwości.
Bardzo polecam panią Natalię, dzięki niej zrobiłam spory progres i poprawiłam oceny.Atmosfera na lekcjach super i bezstresowo☺️ serdecznie polecam!
Pełen profesjonalizm. Córka jest bardzo zadowolona z zajęć 🙂 Cyt. "Pani wszystko spokojnie tłumaczy".
Syn skończył lekcję z entuzjazmem , co nie często się zdarza . Nie tylko zrozumiał lekcję co nie było to dla niego nudne ani trudne
Moi synowi pracują z Panem Norbertem od ok. 6 miesięcy i wszyscy jesteśmy bardzo zadowoleni. Dzieciaki bardzo szybko usystematyzowały swoją matematyczną wiedzę i zrozumiały dotychczas niejasne, bądź bardziej skomplikowane tematy. Obaj chętnie uczestniczą w lekcjach, a po zakończonych zajęciach zawsze widać w nich satysfakcję. Z mojej strony jako rodzica bardzo dziękuję za doskonały kontakt i współpracę. Bardzo serdecznie polecam,
Bardzo dobry nauczyciel z pasją podchodzi do lekcji potrafi zachęcić ucznia do matematyki.
To była nasza pierwsza lekcja z Natalią i NA PEWNO nie ostatnia. Wspaniałe podejście do ucznia. Stosowanie wielu metod nauczania w zależności od potrzeb na daną chwilę. Podpowiadanie trików w razie potrzeby, które uczeń może zastosować w stresujących sytuacjach. Wspaniała osoba i wspaniały nauczyciel.
polecam bardzo pana krystiana, nie stresuje mnie jak jego poprzednicy i ma ogromna cierpliwość (;
Matematyka z tym nauczycielem to sama przyjemność. Jest super. Odkąd syn zaczął się z nim uczyć, to nie może się doczekać kolejnej lekcji.
Pan Adam wyróżnia się ogromną cierpliwością oraz zaangażowaniem. Skutecznie motywuje do pracy i rozwijania umiejętności. Lekcje odbywają się w spokojnej i przyjaznej atmosferze, co sprawia, że nie boje zadawać się pytań. Dzięki jego wsparciu matematyka staje się bardziej zrozumiała :).
Nauczycielka bardzo sympatyczna z świetnym podejściem do Córki. Oliwia bardzo zadowolona z lekcji diagnostycznej. Pierwszy raz od razu zrozumiała tłumaczenia p. Nauczycielki. Kontynuujemy dalszą naukę z panią Natalią.
Polecam lekcje z Panem Maciejem. Syn miał trudności w szkole, był bardzo zniechęcony co matematyki. Po kilku lekcjach nastąpiła ogromna zmiana w jego podejściu do zadań, chętnie pracował i ma poprawioną ocenę na semestr 🤩 wzrosła jego samoocena i wiara w siebie, chęć do matmy, co przy adhd nie jest tak łatwe do osiągnięcia. Także bardzo polecamy mathema.me z Panem Maciejem.
Syn jest po pierwszej lekcji i jest zadowolony bardzo miła i sympatyczna pani ma podejście do ucznia polecam
Syn bardzo zadowolony z korepetycji i zaproponował lekcje 2x w tygodniu.
Pan Jakub to znakomity nauczyciel matematyki, który wyróżnia się ogromnym zaangażowaniem i pasją do nauczania. Potrafi w przystępny sposób tłumaczyć nawet najtrudniejsze zagadnienia, dzięki czemu lekcje są zrozumiałe i ciekawe. Zawsze jest cierpliwy, pomocny i życzliwy wobec uczniów, motywując ich do pracy i wiary we własne możliwości. Dzięki niemu matematyka staje się logiczna, mniej stresująca i naprawdę interesująca.
Pan Prowadzący ma świetne podejście do dzieci - potrafi rewelacyjnie tłumaczyć w sposób prosty i rzeczowy, ma anielską cierpliwość. Synek zachwycony! Zdecydowanie baaardzo polecam!
lekcje nie wywołują stresu. zadania są dobrane w idealny sposób. W prosty sposób wytłumacza ciężkie rzeczy. W miłej atmosferze są prowadzone zajęcia
Pani Marta Tobolik tworzy pozytywną atmosferę podczas lekcji. Potrafi dostrzec braki i z dużą cierpliwością dąży do ich uzupełnienia. Mój syn chętnie bierze udział w lekcjach i mówi, że Pani Marta dobrze tłumaczy. Polecam Panią Martę Tobolik jako nauczyciela matematyki.
Polecam.
Z całego serca polecam tego nauczyciela. Zajęcia są prowadzone w przyjaznej i bezstresowej atmosferze, a materiał tłumaczony jasno, cierpliwie i w sposób dopasowany do ucznia. Dzięki korepetycjom zauważyłam realne postępy. Nauczyciel jest zaangażowany, punktualny i zawsze dobrze przygotowany. Zdecydowanie warto!
Bardzo dobry korepetytor z matematyki — tłumaczy jasno, cierpliwie i krok po kroku. Potrafi w prosty sposób wyjaśnić nawet trudne zagadnienia i zawsze upewnia się, że materiał jest zrozumiały.
Bardzo polecam ! Świetne podejście do ucznia, wszystko tłumaczone jasno i cierpliwie. Zajęcia są dobrze zorganizowane i naprawdę pomagają zrozumieć materiał.
Lekcja przebiegła w spokojnej i miłej atmosferze. Pani Natali zachęciła do pytań i otwartości. Emilka była bardzo zadowolona 🙂
Krystian korepetytor od matematyki jasno tłumaczy materiał i zawsze cierpliwie odpowiada na pytania. Na lekcjach panuje dobra i luzna atmosfera, dzięki łatwo się skupić i zrozumieć nowe zagadnienia.
Korepetytor tłumaczy w prosty i zrozumiały sposób, jasno, cierpliwie i z zaangażowaniem.
Pan Sebastian wyróżnia się ogromną cierpliwością i umiejętnością tłumaczenia trudnych zagadnień w prosty, zrozumiały sposób. Zajęcia zawsze są dobrze zorganizowane i prowadzone w przyjaznej atmosferze, dzięki czemu nauka staje się dużo łatwiejsza i bardziej motywująca. Polecam!
Pan Sebastian to bardzo dobry nauczyciel. Dzieki jego pracy, moj syn niw boi sie lekcji matematyki no i oceny znacznie ulwgly poprawie. Bardzo polecam, bardzo kompetentny nauczyciel. Cala wiedza przekazana podczas lekcji zostaje w glowie ucznia😊
Cierpliwy, potrafi jasno i prosto wytłumaczyć materiał, oraz posiada bardzo przyjazne i bezstresowe podejście do ucznia
Ten czlowiek mnie ratuje z matematyki i ogolnie mega dobrze sie z nim pracuje bo jest cierpilwy oraz ma duza wiedze z tego przedmiotu
Szczerze polecam w szczególności Pana Kamila. Dokonał cudu 😀😃🙂, rozkochał w matematyce, wytlumaczył, nauczył i dodał pewności siebie wyjątkowemu "antymatematykowi", jeszcze raz szczerze polecam:)
Jestem bardzo zadowolona z zajęć w Mathema , a zwłaszcza za umiejętność przekazania wiedzy i zrozumiałe wytłumaczenie przez Pan Marcina Przegalińskiego. Dla syna to najlepszy nauczyciel matematyki jakiego do tej pory spotkał Lekcje przez Pana Marcina są prowadzone w bardzo przejrzysty sposób i na bardzo fajnych przykładach tłumaczy zadania. Polecamy naukę u Pana Marcina Przegalińskiego.
Bardzo fajnie przeprowadzona lekcja. Dziękuję w imieniu syna.
Uczeń zadowolony z lekcji, rozumie zagadnienia, jednak nie moze tego przełożyć na warunki szkolne.
Brak umiejętności jasnego tłumaczenia zadań. Brak przygotowania metodycznego. Prowadząca nie jest nauczycielem matematyki. Nie ma wykształcenie w tym kierunku.
Pani jest bardzo wspaniałą osobą, ma świetne podejście do mojego dziecka. Uczy na wysokim poziomie. Jest wymagająca, ale w dobrym znaczeniu tego słowa - potrafi wytłumaczyć w spokoju, tak by dziecko potrafiło wykonać zadanie samo z zaangażowaniem swojego myślenia. Jestem zadowolona jako matka, a Olga czeka z zaciekawieniem na każdą kolejną lekcje, a to jest najważniejsze !
Jasno i wyraźnie Pan Pawel przekazywał wiedzę, nawet jak potrzeba było kilka razy powtórzyć to bez nerwów powtarzał i wyjaśniał..
Dziękujemy Panu Adrianowi Kaczyńskiemu za profesjonalną lekcję. Córka jest bardzo zadowolona i zdecydowała się na współpracę z Panem Adrianem w uczeniu się matematyki. Magda
Relacja z uczniem i jakość prowadzenia zajęć.
Bardzo dobrze podejscie do dziecka. Dziękujemy bardzo.
Wspaniala oraz ciepła nauczycielka. Nauka z Panią Klaudia to sama przyjemność 🤩
Córce lekcja się podobała, z chęcią zobaczy się na kolejnych lekcjach z Panem Adrianem Dziękujemy :)
Polecam. Syn jest zadowolony, zajęcia są bezstresowe.
Pani Klaudia ma super podejście do młodzieży, swoim indywidualnym podejściem potrafi zainteresować każdego
Lekcja córce się bardzi podobała. Bardzo polecam.
Bardzo fajne pan cypian prowadzi zajęcia

Wybierz abonament dopasowany do tempa i celów nauki
Im więcej lekcji — tym niższa cena za zajęcia i szybszy postęp

- ✅Szybko nadrabia zaległe tematy
- ✅Pierwsze "aha!" — łatwy start
- ✅Dostęp do asystenta AI
- ✅Quizy po każdej lekcji
- ✅Podstawowe wsparcie użytkowników
- ✅Gwarantowany postęp w programie nauczania
- ✅Osobista ścieżka nauki
- ✅Dostęp do asystenta AI
- ✅Quizy po każdej lekcji
- ✅Rozszerzone wsparcie + rekomendacje nauczyciela
- ✅Wyraźny skok — od "boję się matmy" do "rozumiem!"
- ✅Przygotowanie do trudniejszych tematów szkolnych i olimpijskich
- ✅Dostęp do asystenta AI
- ✅Zaawansowane quizy i zadania adaptacyjne
- ✅Priorytet w rezerwacji czasu u nauczyciela
- ✅Najkorzystniejsza cena za lekcję
- ✅Pełny cykl nauki z wyraźnymi rezultatami
- ✅Dostęp do asystenta AI
- ✅Zaawansowane quizy i zadania adaptacyjne
- ✅Maksymalny poziom wsparcia i osobistych rekomendacji
Odpowiadamy na wasze "a co jeśli?"
Wszystkie lekcje odbywają się online w formacie indywidualnych zajęć między uczniem a nauczycielem. Pracują razem przez Zoom lub Google Meet: rozwiązują zadania, omawiają przykłady i krok po kroku dochodzą do zrozumienia tematu. Format jest wygodny i elastyczny — bez pośpiechu i presji, z naciskiem na zrozumienie. Do zajęć wystarczy telefon, tablet lub komputer z dostępem do internetu i kamerą. Nauczyciele mogą korzystać z interaktywnych tablic do wyjaśnień, dlatego w miarę możliwości zalecamy wybór urządzenia z większym ekranem.
Tak, zalecamy włączanie kamery i mikrofonu podczas lekcji. Dzięki temu nauczyciel łatwiej wyczuwa nastrój dziecka, w porę zauważa, gdzie potrzebna jest pomoc, i utrzymuje żywy kontakt. Jeśli pojawią się trudności techniczne — nie martw się. Zawsze znajdziemy wygodne rozwiązanie razem.
Proponujemy odpowiedzieć na kilka pytań, aby zrozumieć, co jest teraz najważniejsze dla waszego dziecka: jego poziom, cele i tematy, z którymi chce się uporać. Na podstawie odpowiedzi proponujemy nauczyciela, który najlepiej pasuje do tego zapotrzebowania i z którym dziecko będzie się czuło spokojnie, zrozumiale i ciekawie. Taki nauczyciel jest oznaczony plakietką "Najlepsza rekomendacja" — co oznacza, że jego doświadczenie dobrze odpowiada waszej sytuacji. Jeśli trudno będzie wam dokonać wyboru, nasz menedżer z przyjemnością pomoże. Według naszych statystyk 95% rodziców jest zadowolonych z dobranego nauczyciela. Jeśli jednak nauczyciel z jakiegoś powodu nie będzie odpowiedni, bezpłatnie dobierzemy innego.
Nauka w naszej szkole zaczyna się od lekcji zapoznawczej — to pełnoprawne zajęcia, których celem jest określenie tematów wymagających szczególnej uwagi, stworzenie indywidualnego planu nauki dla waszego dziecka, a także zapoznanie się z nauczycielem i przygotowanie dziecka do komfortowej nauki. Po lekcji nauczyciel przygotowuje raport dla rodziców i spersonalizowany plan zajęć, aby nauka była zrozumiała, komfortowa i jak najbardziej efektywna.
Obecność rodziców nie jest wymagana. Na pierwszej lekcji zapoznawczej przydatne będzie, jeśli możecie dołączyć na ostatnie minuty, aby usłyszeć opinię zwrotną i zadać pytania nauczycielowi. Jeśli nie ma takiej możliwości, możecie zapoznać się z raportem i planem dalszej nauki na platformie. Podczas regularnych lekcji zalecamy, aby dziecko uczyło się samodzielnie z nauczycielem. Dzięki temu łatwiej się skupia, buduje kontakt i stopniowo czuje pewność we własnej nauce.
Tak, możesz zmienić nauczyciela w każdej chwili. Można to zrobić samodzielnie w panelu osobistym lub kontaktując się z czatem wsparcia na platformie.
Standardowy czas trwania lekcji to 55 minut. To wystarczający czas, aby dobrze wyjaśnić materiał, utrwalić temat i odpowiedzieć na wszystkie pytania dziecka bez przeciążania.
Lekcja zapoznawcza kosztuje 49 zl. W przypadku programów specjalnych — 79 zl. Cena lekcji zaczyna się od 79 zl, w zależności od wybranego abonamentu i poziomu nauczyciela. Im większy pakiet lekcji wybierzesz, tym korzystniejsza cena za lekcję.
Tak, jeśli chcesz, możesz wstrzymać naukę na okres do 180 dni. Wszystkie lekcje zostają na saldzie, a po wznowieniu dziecko kontynuuje od momentu, w którym się zatrzymało.
Tak. Jeśli wasze plany się zmieniły, możecie samodzielnie przełożyć lub odwołać lekcję w swoim panelu lub skontaktować się ze wsparciem. Uwaga: w przypadku nieobecności bez wcześniejszego powiadomienia lekcja zostanie odjęta z waszego salda. Zalecamy wcześniejsze informowanie o zmianach, aby zachować lekcję.



