
Learn mathematics
at the school
of mathemagic
Still falling behind?

Magic of understanding

Magic of understanding

Online that captivates
We teach so the child truly understands
Live 1:1 explanation
The tutor doesn't just read material — they lead a dialogue. Explains through examples, asks questions, draws diagrams, adapts to the child's pace.
No pressure

Students love the format
Interactive lessons — in the rhythm of today's child
Lessons are designed to keep interest. Children feel progress after the very first sessions — and want to continue.
Video call + interactive

Support between lessons
The child is never left alone with a difficult topic. The AI assistant helps figure things out step by step, and the tutor supports and guides in the right direction.
Online that captivates
We teach so the child truly understands
Live 1:1 explanation
The tutor doesn't just read material — they lead a dialogue. Explains through examples, asks questions, draws diagrams, adapts to the child's pace.
No pressure

Students love the format
Interactive lessons — in the rhythm of today's child
Lessons are designed to keep interest. Children feel progress after the very first sessions — and want to continue.
Video call + interactive

Support between lessons
The child is never left alone with a difficult topic. The AI assistant helps figure things out step by step, and the tutor supports and guides in the right direction.

The path to results — in simple steps
These aren't abstract "weekly lessons" — it's a personal learning path your child follows together with a tutor and AI assistant

Introductory lesson

We explore the child's thinking, gaps and strengths. In a light, inspiring atmosphere — like a friendly chat, not an exam.
Sign upPersonal action plan


We create a specific plan: what to study, in what order, what to focus on. No chaos — just clear logic and structure that's easy to follow.
Sign up1:1 lessons + AI assistant + quizzes

The child learns through live dialogue with the tutor, and between lessons reinforces the material with: short quizzes, AI assistant explanations, micro-tasks.
Sign upVisible progress
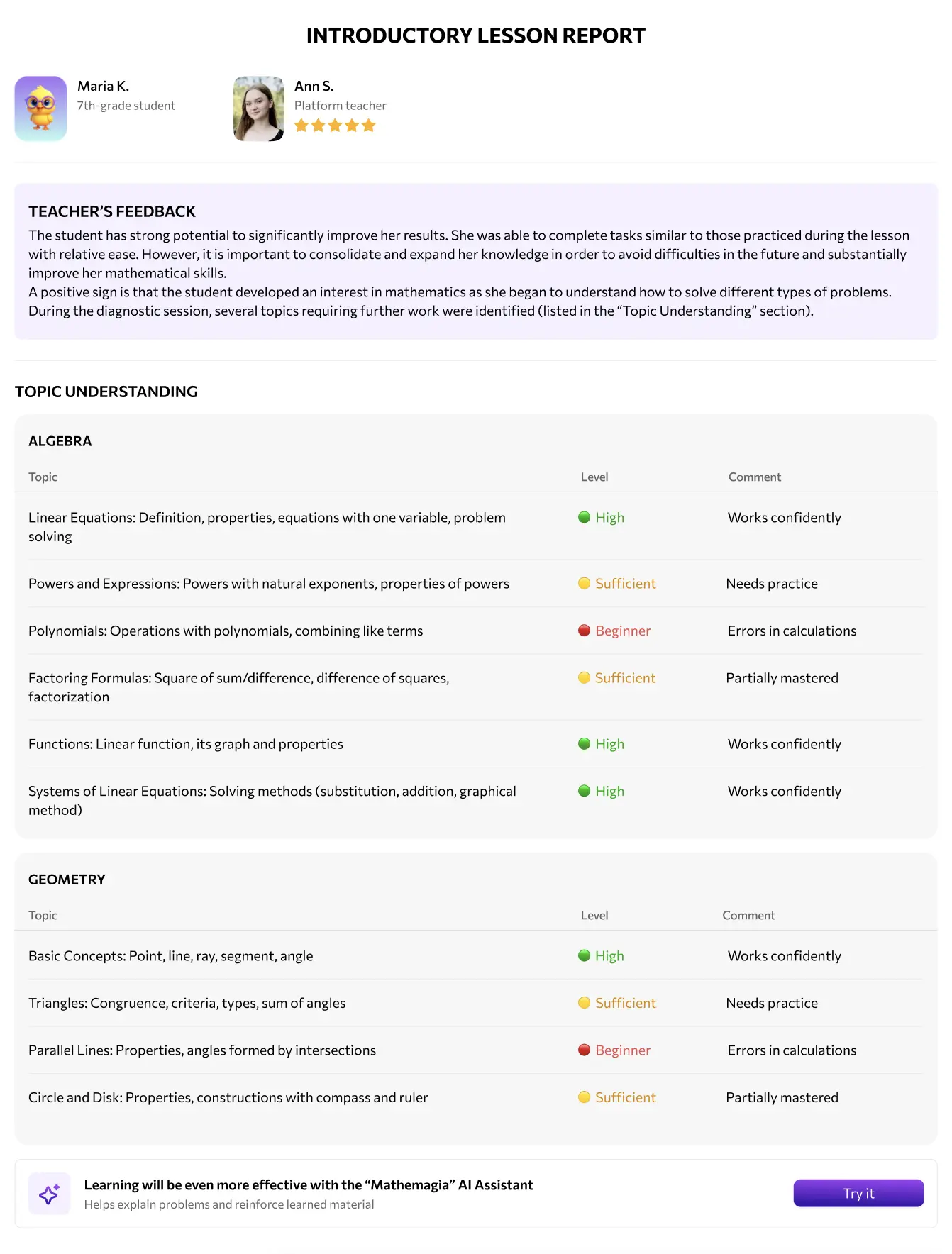

Parents receive a short report: what was done, successes, recommendations. And the child sees they can do more than they thought.
Sign upAI assistant: explains, guides, supports
It's like having a personal teacher 24/7: you ask and immediately get a clear explanation. No stress. No rush. At the child's pace
AI assistant: explains, guides, supports
It's like having a personal teacher 24/7: you ask and immediately get a clear explanation. No stress. No rush. At the child's pace
Quizzes — easy reinforcement of knowledge that students love



Short, interactive, designed so that the child doesn't just recall material, but feels a small victory every time they get it "right"
✅ 3–5 minutes — and the topic is reinforced
Perfect for quickly reviewing a topic or testing yourself after homework
😎 Made a mistake? Get an explanation
Mistakes aren't scary here — they lead to "aha, now I get it!"
🚀 A daily habit that brings so many benefits
Small steps that build confidence.
Quizzes — easy knowledge reinforcement that students love
Short, interactive, designed so that the child doesn't just recall material, but feels a small victory every time they get it "right"
✅ 3–5 minutes — and the topic is reinforced
Perfect for quickly reviewing a topic or testing yourself after homework
😎 Made a mistake? Get an explanation
Mistakes aren't scary here — they lead to "aha, now I get it!"
🚀 A daily habit that brings so many benefits
Small steps that build confidence.
Mathema builds the habit of thinking confidently
Short quizzes, AI assistant tips, regular lessons — it's a system that shapes not just grades, but mathemagical thinking.

Logical thinking skill — a universal superpower

Comfortable pace, personalized approach

The feeling of victory: every "correct!" — like a small win
Mathema builds the habit of thinking confidently
Short quizzes, AI assistant tips, regular lessons — it's a system that shapes not just grades, but mathemagical thinking.

Logical thinking skill — a universal superpower

Comfortable pace, personalized approach

The feeling of victory: every "correct!" — like a small win
Answering your "what ifs?"
All lessons are conducted online in a one-on-one format between the student and teacher. They work together via Zoom or Google Meet: solving problems, discussing examples, and reaching understanding step by step. The format is convenient and flexible — no rush or pressure, with a focus on understanding. A phone, tablet, or computer with internet access and a camera is all you need. Teachers may use interactive whiteboards for explanations, so we recommend choosing a device with a larger screen when possible.
Yes, we recommend turning on the camera and microphone during the lesson. This helps the teacher better sense the child's mood, notice where help is needed, and maintain a live connection. If there are technical difficulties — don't worry. We'll always find a convenient solution together.
We suggest answering a few questions to understand what matters most for your child right now: their level, goals, and topics they want to work on. Based on your answers, we suggest a teacher who best fits this request and with whom the child will feel calm, understood, and interested in learning. Such a teacher is marked with a "Best recommendation" badge — meaning their experience matches your situation well. If you find it hard to choose, our manager will gladly help. According to our statistics, 95% of parents are satisfied with the selected teacher. However, if the teacher doesn't suit for any reason, we'll find another one for free.
Learning at our school starts with an introductory lesson — a full session aimed at identifying topics that need special attention, creating an individual learning plan for your child, as well as getting acquainted with the teacher and setting the child up for comfortable learning. After the lesson, the teacher prepares a report for parents and a personalized lesson plan to make learning clear, comfortable, and as effective as possible.
Parental presence is not required. During the first introductory lesson, it's helpful if you can join for the last few minutes to hear feedback and ask the teacher questions. If that's not possible, you can review the report and the learning plan on the platform. During regular lessons, we recommend that the child works independently with the teacher. This helps them focus better, build rapport, and gradually feel confident in their own learning.
Yes, you can change your teacher at any time. You can do this on your own in your personal account or by contacting the support chat on the platform.
The standard lesson duration is 55 minutes. This is enough time to properly explain the material, reinforce the topic, and answer all the child's questions without overloading.
The introductory lesson costs 40 GBP.
Yes, if you wish, you can pause learning for up to 180 days. All lessons are kept on your balance, and after resuming, the child continues from where they left off.
Yes. If your plans have changed, you can reschedule or cancel a lesson on your own in your account, or contact support. Please note: in case of a no-show without prior notice, the lesson will be deducted from your balance. We recommend notifying us of changes in advance to preserve your lesson.

